démontrable

démontrable [ demɔ̃trabl ] adj.

• demonstrable v. 1265; de démontrer

♦ Qui peut être démontré. Proposition démontrable (⇒ décidable) . — Math Énoncé démontrable, qui possède une démonstration formelle. ⊗ CONTR. Indémontrable.

● démontrable adjectif Qui peut être démontré.

démontrable

adj. Qui peut être démontré.

⇒DÉMONTRABLE, adj.

Qui peut être démontré. Cette proposition est démontrable (Ac.) :

• Quand bien même il l'[la vierge] aurait vue seulement en rêve, sa guérison du moins était là, indéniable, démontrable, miraculeuse assurément.

GIDE, Les Caves du Vatican, 1914, p. 703.

Rem. On rencontre ds la docum., démonstrabilité, subst. fém. (fait sur le rad. de démonstration). Possibilité d'être démontré, dont le synon. démontrabilité est attesté ds les dict. La démonstrabilité de l'existence de Dieu par les œuvres divines paraît être une doctrine révélée (Théol. cath. t. 4, 1 1920, p. 927).

Prononc. et Orth. :[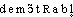]. Ds Ac. dep. 1718. — Étymol. et Hist. 1269-78 demonstrable (Rose, éd. F. Lecoy, 4250). Dér. de démontrer; suff. -able. Fréq. abs. littér. :30.

démontrable [demɔ̃tʀabl] adj.

ÉTYM. V. 1273, demonstrable; de démontrer, et -able.

❖

♦ Qui peut être démontré. || Proposition démontrable.

❖

CONTR. Indémontrable.

DÉR. Démontrabilité.

Encyclopédie Universelle. 2012.